Everlasting Privacy for VCs

What we need from a privacy enhancing signature scheme and why

Dr. Greg M. Bernstein

2025-10-23

Introduction

Who Am I

What’s This about?

  • Everlasting Privacy for credentials in privacy critical applications
  • Mitigating Attacks on privacy of credentials
  • Mitigating Attacks on Security of credentials with enhanced privacy
  • Impacts and mitigation of Cryptographically Relevant Quantum Computer (CRQC)
  • Viability of early deployment via VC Data Integrity mechanisms

Privacy Requirements

Data Minimization

“it’s none of your business”, “they don’t need to know that”, …

Not “I’ve got nothing to hide..”

  • Put the least possible amount of information into a VC. Issue multiple VC over separate data.
  • Support selective disclosure VC-DI-ECDSA-SD and VC-DI-BBS

Tracking, Linkages, and It’s Prevention

Bloom County November 5, 2009

A whole lot of “data sharing” going on

Current Browser and App Based Tracking

Tracking for Security I

Ebb tide, wind lulls…

Tracking for Security II

Tracking for Safety

Tracking for Security III

Enterprise Single Sign On (SSO)

  • Tracking adversaries Lateral Movement
  • In OpenID there is the user, relying party (RP) (resource user wants access to), and the identity provider (IDP). The IDP has information/history on all logins to RPs and hence can detect unusual patterns characterizing lateral movement.
  • Using a SSO such as a variant of OpenID on the public Internet means handing over your site visit history to the IDP, i.e., giving up your privacy.

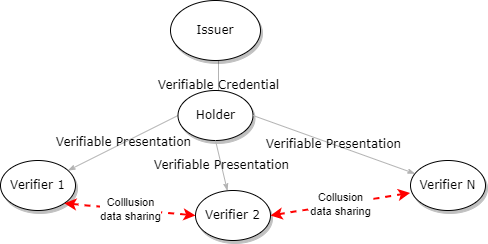
Tracking with Verifiable Credentials 1

Verifier-Verifier Collusion

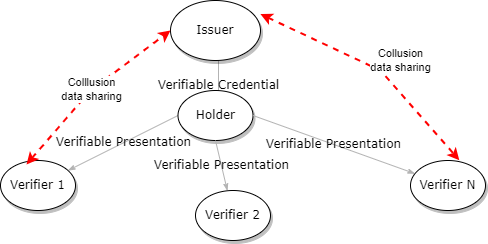
Tracking with Verifiable Credentials 2

Verifier-Issuer Collusion

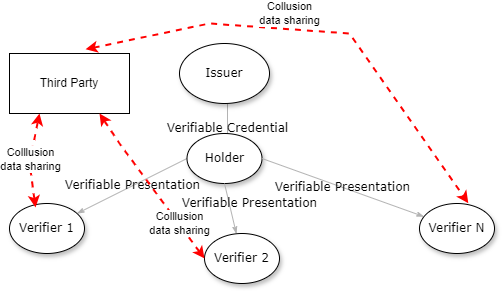
Tracking with Verifiable Credentials 3

Verifier - Third Party Collusion

Digital Signature Artifacts as Tracking Cookies

  • If used, Holder public key data is essentially unique
  • EdDSA, ECDSA, BBS signatures (not proofs) all are based on algorithms that are very sensitive to input data, and hence will amplify the uniqueness of any input data.

Security Requirements

Security Overview

  1. Forgery prevention – the core of a digital signature scheme
  2. Replay protection
  3. Credential Theft prevention – public key binding (trackable), or anonymous holder binding
  4. Credential Abuse mitigation– Complicit holder, Pseudonyms

Forgery Prevention

EUF-CMA (existential unforgeability under chosen message attacks) is usually the minimal security property required of a signature scheme. It guarantees that any efficient adversary who has the public key \(pk\) of the signer and received an arbitrary number of signatures on messages of its choice (in an adaptive manner): \(\{m_i, \sigma_i\}_{i=1}^N\), cannot output a valid signature \(\sigma^∗\) for a new message \(m^∗ \notin \{m_i\}_{i=1}^N\) (except with negligible probability). In case the attacker outputs a valid signature on a new message: \((m^∗, \sigma^∗)\), it is called an existential forgery.

Forgery Prevention and Beyond

From VC-DI-EdDSA types of signature security

  • EUF-CMA (existential unforgeability under chosen message attacks)
  • SUF-CMA (strong unforgeability under chosen message attacks)
  • Binding signature (BS)
  • Strongly Binding signature (SBS)

Replay Prevention

  • Wikipedia “A replay attack (also known as a repeat attack or playback attack) is a form of network attack in which valid data transmission is maliciously or fraudulently repeated or delayed.”
  • PacketLabs: Your Guide to Replay Attacks
  • Caution: Some mitigation approaches require unique identifiers or public keys

BBS Replay Protection (holder -> verifier) 1

BBS Replay Protection (holder -> verifier) 2

No holder identifying information needed!

Mitigating Stolen Credentials: Public Key Based Holder Binding I

Holder Binding based on Public Key Cryptography

  1. Holder generates a public/private key pair for creating digital signatures, such as for ECDSA signatures.
  2. The public key is sent to the issuer for inclusion in the credential that is sent to the holder.

Mitigating Stolen Credentials: Public Key Based Holder Binding II

  1. When requesting the credential the verifier also includes a message acting as a test. The holder signs this message with their private key and includes it with the credential sent to verifier.
  2. The verifier then validates the signature on the test message with the holder’s public key contained in the VC and it verifies the signed credential with the issuer’s public key.
  3. Holder’s Public Key acts as a tracking cookie breaking privacy

Mitigating Stolen Credentials: Public Key Based Holder Binding Flow III

Mitigating Stolen Credentials: BBS Anonymous Holder Binding

  • Holder generates and securely stores a secret
  • Holder makes a Pedersen commitment to the secret
  • Holder sends commitment and ZKP of secret (not the secret) to Issuer
  • Issuer blind signs Holder secret via commitment and includes it with credential signature

Mitigating Stolen Credentials: Anonymous Holder Binding Flow

Credential Abuse: Complicit Holder 1

sequenceDiagram
    participant Issuer
    participant Holder
    participant Abuser as Credential Abusers (N)
    participant Verifier
    Holder ->> Holder: Generates Secret
    Holder ->> Issuer: Commitment to Secret with proof
    Issuer ->> Holder: VC BBS blind signed on Commitment
    Abuser ->> Holder: Can you give me access? I'll make it worth your while...
    Holder ->> Holder: Generates BBS Proof with secret
    Holder ->> Abuser: Here ya go buddy -- BBS SD VC
    Abuser ->> Verifier: BBS SD VC

Credential Abuse: Complicit Holder 2

  • Privacy enhanced credential is completely anonymous
  • Credential is strongly bound to Holder
  • But Holder is complicit (evil) and allowing or profiting from others use of its credential.
  • Sometimes we call this a Sybil attack, though this isn’t quite the same situation.

Credential Abuse Mitigation 1: Cryptographic Pseudonyms

  • Include a per Verifier cryptographic pseudonym along with the credential
  • Include ZKP that pseudonym was properly computed based on “verifier context” and an ordered, fixed length set of holder “nym secrets” signed by the Issuer
  • For privacy pseudonyms across different verifiers must unlinkable

Credential Abuse Mitigation 2: BBS Pseudonyms

From BBS Pseudonyms Pseudonym Calculation Procedure

// Vector of size N of nym_secrets
OP = hash_to_curve_g1(context_id) // a point in the curve group G1
z = hash_to_scalar(context_id)
poly = sum i = 0 to N-1 of nym_secrets[i]*z^i // in the scalar field
pseudonym = OP*poly // in the curve group G1

Privacy Preserving Credential Solution

  • ZKP from Holder to Verifier to assert signature from issuer (with privacy preserving anti-replay support)
  • Anonymous holder binding to prevent credential theft (credential tied to holder secret not holder public key)
  • Pseudonyms to allow holder to assert identity and reduce threat of credential abuse (holder as an accomplice in credential reuse)

Everlasting Privacy…

Notions of Cryptographic strength

  1. Informational Theoretic/Perfect
  2. Computational (based on hard problems)
  3. Concrete (furnishing actual number estimates)

Example: Perfect Secrecy (information theoretic)

  • Theorem (Katz & Lindell): The one-time pad encryption scheme is perfectly secret
  • The definition of perfectly secret can be cast in terms of the equivalence of probabilities or indistinguishability.
  • Theorem (Katz & Lindell): For an encryption scheme to be perfectly secret then the encryption keys must be longer than the messages. ==> perfectly secret encryption schemes are not very practical.

Computational Security

From Katz and Lindell

  • “Security is only guaranteed against efficient adversaries run for some feasible amount of time”
    • Hence why cryptography is interested in computationally “hard” problems
  • “Adversaries can potentially succeed with some very small probability”
    • Achieving zero probability in many contexts is impossible, achieving \(2^{-128} = 3 \times 10^{-39}\) is reasonable.

Example: Forward Secrecy

From Wikipedia: Forward secrecy

“In cryptography, forward secrecy, is a feature of specific key-agreement protocols that gives assurances that session keys will not be compromised even if long-term secrets used in the session key exchange are compromised, limiting damage.”

  • Based on Diffie-Hellman key agreement protocol which is related to the “hard” discrete log problem.
  • Some protocols that support (in some form) perfect forward secrecy: SSH, TLS, Signal (double ratchet). This is one of the big uses of ephemeral keys.

Informational and Computational Example: Commitment Schemes 1

From Wikipedia: Commitment Scheme

“A commitment scheme is a cryptographic primitive that allows one to commit to a chosen value (or chosen statement) while keeping it hidden to others, with the ability to reveal the committed value later. Commitment schemes are designed so that a party cannot change the value or statement after they have committed to it: that is, commitment schemes are binding.”

Informational and Computational Example: Commitment Schemes 2

From Wikipedia: Commitment Scheme

  • “Formal definitions of commitment schemes vary strongly in notation and in flavour. The first such flavour is whether the commitment scheme provides perfect or computational security with respect to the hiding or binding properties.”
  • “The two most important combinations of these properties are perfectly binding and computationally hiding commitment schemes and computationally binding and perfectly hiding commitment schemes. Note that no commitment scheme can be at the same time perfectly binding and perfectly hiding.”

Informational and Computational Example: Commitment Schemes 3

  • Blind BBS signatures and BBS Pseudonyms make use of Pedersen commitments
  • From J. Camenisch and A. Lysyanskaya, “Signature Schemes and Anonymous Credentials from Bilinear Maps,” in Advances in Cryptology – CRYPTO 2004. “This (the Pedersen) commitment scheme is information theoretically hiding, and is binding under the discrete logarithm assumption.”

Quantum Mechanics

  • The fascinating world of Quantum Mechanics, also see the theoretical minimum, by Leonard Susskind for a clear but rigorous minimalistic introduction.
  • Stern–Gerlach experiment, 1922. The first demonstration of a quantum bit? Qubit
  • 2025 Physics Nobel Prize John Clarke, UC Berkeley emeritus professor, awarded 2025 Nobel Prize in Physics. The Nobel Prize committee honored Clarke “for the discovery of macroscopic quantum mechanical tunneling and energy quantization in an electric circuit.” These circuits were forerunners of the qubits in many quantum computers.

Quantum Attacks

From Wikipedia: Quantum Attacks

  • “Most quantum attacks on symmetric ciphers provide a square-root speedup to their classical counterpart, thereby halving the security level provided. For example, AES-256 would provide 128 bits of quantum security, which is still considered plenty.”
  • “Shor’s algorithm promises a massive speedup in solving the factoring problem, the discrete logarithm problem, and the period-finding problem, so long as a sufficiently large quantum computer on the order of millions of cubits is available. This would spell the end of RSA, DSA, DH, MQV, ECDSA, EdDSA, ECDH, and ECMQV in their current forms.” ==> Meaning of a Cryptographically Relevant Quantum Computer (CRQC).

Implications of CRQC

  1. ECDSA, EDDSA, Schnor EC, and BBS signatures: could be forged
  2. Traditional key encapsulation mechanisms (KEM) can be broken
  3. Note that “public key encryption/decryptions” is based on a KEM + symmetric encryption alg.
  4. Information theoretic/perfect security not affected, e.g., information theoretic hiding in Pedersen

Preparing for CRQC

Why now? Protection against “harvest now, decrypt later”

  1. New KEM algorithms, but since they are new how much should we trust them?
  2. New Digital signature algorithms
  3. Hybrid KEMs combine pre and post quantum KEMs in a way that should only “break” if both are hacked
  4. Sign the same “document” with both pre and post quantum Digital Signatures (EUF), then only can forge if can forge both signatures. VC Data Integrity supports multiple signatures (“proofs”) so we are ready to go. Just need to add new cryptosuites.

Privacy of BBS with a CRQC

  • “BBS proofs” have everlasting unlinkability (BBS Signatures: Post-quantum security)
  • Pedersen commitments used between Holder and Issuer in Blind BBS and BBS Pseudonyms are perfectly hiding so no leakage of secrets to a CRQC
  • Pseudonyms can be perfectly unlinkable under constrained use, and may be computationally infeasable in general widespread use.

BBS Proofs: Post-quantum security

From: BBS Signatures: Post-quantum security

“On the other hand, data confidentiality cannot be broken, even by adversaries with unbounded computational resources and in possession of the Signer’s secret key. This means that even by utilizing a CRQC, adversaries will not be able to compromise the data confidentiality property of BBS proofs. As a result, an adversary with access to such a quantum computer, will not be able to reveal either the messages undisclosed by a BBS proof, or the hidden signature value (which the Prover showcases possession of). This guarantees that the privacy and hiding properties of BBS proofs that are currently used, will not be compromised by future quantum-attacks (a property that is often referred to as everlasting privacy). Note that this only considers BBS proofs, not BBS signatures, which do not possess the same hiding properties as the BBS proofs.”

Pseudonym Computation

  • \(OP \in \mathbb{G}_1\), \(OP = \text{hash_to_curve_g1}(\text{context_id})\) where context_id is public information from the Verifier
  • \(z \in \mathbb{F}_r\), \(z = \text{hash_to_scalar}(\text{context_id})\)
  • \(pseudonym \in \mathbb{G}_1\)
  • \(pseudonym = OP^{(\sum_{i = 0}^{N-1} \text{nym_secrets}[i]\cdot z^i)}\)

* Note \(r = 0x73eda753299d7d483339d80809a1d80553bda402fffe5bfeffffffff00000001\)

Pseudonym from a single secret is Vulnerable to CRQC

  • \(pseudonym = OP^{(\text{nym_secret}\cdot z)}\)
  • CRQC can take discrete log: \(log(pseudonym) = {\text{nym_secret}\cdot z \cdot}log(OP)\)
  • Reveals \(\text{nym_secret} = z \cdot log(OP)/log(pseudonym)\) since \(z\) and \(OP\) are known.

Pseudonym from N secrets with CRQC Part 1

  • If you don’t have pseudonyms values from N different contexts/verifiers, then you cannot determine the nym secrets with a CRQC, i.e., under determined system of equations
  • Easy for a wallet to know how many different contexts/verifiers since it has to compute the pseudonym and proof.
  • Everlasting privacy for pseudonyms created from credential in up to N-1 different contexts. Note you can return to the same context as many times as desired without impacting “number of uses”.

Pseudonym from N secrets with CRQC Part 2

Additional thoughts…

  • Even with a CRQC and collusion of many verifiers it is still not so simple to reverse engineer nym secrets for a particular holder
  • You don’t know before hand which pseudonyms belong to which holders (that’s the whole point)
  • Must collect all pseudonyms from all holders and then try to process
  • But if there are many holders we don’t which nym secrets belong to which and hence haven’t reduced the anonymity set…

Additional Costs of N nym secrets

  • Increases length proof of commitment (Holder -> Issuer) and proof of signature/pseudonym (Holder -> Verifier) by 32*N bytes, where 32 is the size of a BBS “scalar”
  • Does not increase size of BBS signature (Issuer -> Holder)
  • Requires additional processing (incrementally proportional to N) for commitment computation, proof generation, proof verification
  • Optimizations to reduce proof sizes are possible (but are not standardized)

Enabling Privacy Enhanced Credentials Now

  1. The BBS Privacy enhanced cryptosuite is just about ready! All needed features are contained in IRTF CFRG working group documents
  2. VC Data Integrity 1.0 supports proofs for multiple cryptosuites, if the privacy enhanced suite (BBS) is not sufficient for all requirements.
  3. User then selects which “proof” to furnish. Default to privacy enhanced with minimal disclosure.

Example of ECDSA and BBS Signed VC

{
  "@context": [
    "https://www.w3.org/ns/credentials/v2",
    "https://w3id.org/citizenship/v4rc1"
  ],
  "type": [
    "VerifiableCredential",
    "PermanentResidentCardCredential"
  ],
  "issuer": {
    "id": "did:key:zDnaeTHxNEBZoKaEo6PdA83fq98ebiFvo3X273Ydu4YmV96rg",
    "image": "data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAAEAAAABCAYAAAAfFcSJAAAADUlEQVQIW2P4z/DiPwAG0ALnwgz64QAAAABJRU5ErkJggg=="
  },
  "name": "Permanent Resident Card",
  "description": "Permanent Resident Card from Government of Utopia.",
  "credentialSubject": {
    "type": [
      "PermanentResident",
      "Person"
    ],
    "givenName": "JANE",
    "familyName": "SMITH",
    "gender": "Female",
    "image": "data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAAEAAAABCAYAAAAfFcSJAAAADUlEQVQIW2P4v43hPwAHIgK1v4tX6wAAAABJRU5ErkJggg==",
    "residentSince": "2015-01-01",
    "commuterClassification": "C1",
    "birthCountry": "Arcadia",
    "birthDate": "1978-07-17",
    "permanentResidentCard": {
      "type": [
        "PermanentResidentCard"
      ],
      "identifier": "83627465",
      "lprCategory": "C09",
      "lprNumber": "999-999-999"
    }
  },
  "validFrom": "2024-12-16T00:00:00Z",
  "validUntil": "2025-12-16T23:59:59Z",
  "proof": [
      {
      "type": "DataIntegrityProof",
      "cryptosuite": "ecdsa-rdfc-2019",
      "created": "2023-02-24T23:36:38Z",
      "verificationMethod": "did:key:zDnaepBuvsQ8cpsWrVKw8fbp---PeNSjVPTWoq6cRqaYzBKVP#zDnaepBuvsQ8cpsWrVKw8fbpGpvPeNSjVPTWoq6cRqaYzBKVP",
      "proofPurpose": "assertionMethod",
      "proofValue": "zaHXrr7AQdydBk3ahpCDpWbxfLokDq---oYm2dyWvpcFVyWooC2he63w1f7UNQoAMKdhaRtcnaE2KTo5o5vTCcfw"
    },
    {
    "type": "DataIntegrityProof",
    "cryptosuite": "bbs-2023",
    "created": "2023-08-15T23:36:38Z",
    "verificationMethod": "did:key:zUC7DerdEmfZ8f4pFajXgGwJoMkV1ofMTmEG5UoNvnWiPiLuGKNeqgRpLH2TV4Xe5mJ2cXV76gRN7LFQwapF1VFu6x2yrr5ci1mXqC1WNUrnHnLgvfZfMH7h6xP6qsf9EKRQrPQ#zUC7DerdEmfZ8f4pFajXgGwJoMkV1ofMTmEG5UoNvnWiPiLuGKNeqgRpLH2TV4Xe5mJ2cXV76gRN7LFQwapF1VFu6x2yrr5ci1mXqC1WNUrnHnLgvfZfMH7h6xP6qsf9EKRQrPQ",
    "proofPurpose": "assertionMethod",
    "proofValue": "u2V0ChVhQhhaN0rXQx8alajD0IS7RFqU97wXQ1nCCB9SDx_8gU676ItJLp2WdYIUmlPjYW-D6Ktw5dMfcTMaLPbF7JCOXUEcQQWLCRQK0FZGHmsJPG7FYQDpbvyXTTZCxjDXNI1e-am9CMB6U_J5S936Tt3PFYUvfjnzCLDGN0glOAtC_BsXXOl26cXYRpA9tG-3F6nwwD9ZYYKTvGvo9pXVJbxIrm3i4wkdhUxqKCTIGrnxFuAdZwWi6T3omD5wzZ7bAGbRneEEQSxBmXtvnC6Pr59nPv_v3HrAW9wq_uxYzF_NyaX3GPv0h_FV2T2OSao8C6uoyWiqIj1ggABEiM0RVZneImaq7zN3u_wARIjNEVWZ3iJmqu8zd7v-BZy9pc3N1ZXI"
  }]
}